LTP voorbereidingspakket
Dit assessment voorbereidingspakket voor LTP is ontwikkeld door ervaren testontwikkelaars en assessment specialisten die voor de grote testleveranciers werken. Je oefent dus gericht met echt relevant en actueel oefenmateriaal. De voorbereidingspakketten van 123test worden aanbevolen door assessment coaches.
Meer zekerheid nodig, vraag ons om advies op maat of probeer enkele gratis voorbeeldtests uit dit pakket.
- Eenmalige betaling
- 90 dagen toegang
- Niet goed, geld terug
- Bekijk hoe het werkt
- review
- review
- review
- Meer reviews
Alle kenmerken van het LTP voorbereidingspakket
- Gegarandeerd hoger scoren op IQ en capaciteitentests
- X categoriëen, Y tests, Z vragen en A vraagstijlen
- Alle vragen ontwikkeld door echte testontwikkelaars
- Uitgewerkte uitleg over de juiste antwoorden
- Instructielessen met oplossingsstrategiëen per categorie
- Oefen waar en wanneer je wilt op PC, tablet of mobiel
- Geschikt voor ontwikkel- en selectie assessments
- Veel gebruikt voor cliënten door trainers en coaches
- Scherpste prijs van Nederland
- Juiste variatie in moeilijkheidsniveaus (gemiddeld hbo/wo)
- Snel inzicht in waar je nog niet goed in bent
- Oefen- of simulatiemodus instelbaar
- Tijdsdruk aan/uitzetten; per test of per vraag
- Gemiddelde tijd per test 12 minuten
- Totale tijdbesteding Q uur
- Je kunt direct starten
Je ontvangt bij je aankoop ook gratis het e-book ‘Alle assessmentgeheimen ontsluierd’ t.w.v. €8,95 (32 pagina’s). 123test ontwikkelt en publiceert al sinds 2003 online loopbaantests, persoonlijkheidstests en IQ en capaciteitentests.
Overeenkomst LTP assessment met voorbereidingspakket
Assessments van LTP worden afgestemd op functie en functieniveau. De variatie in vraagformats en moeilijkheidsniveaus van het LTP voorbereidingspakket dekken de volledige lading daarvan. Alle logica die je kunt verwachten bij een LTP assessment kun je oefenen, en ook in zeer vergelijkbare stijl. Het oefenmateriaal is natuurlijk niet exact identiek maar vormt de nauwkeurige oefening en simulatie waardoor je gegarandeerd hoger zult scoren.
LTP tests en overeenkomstige oefenreeksen
Hieronder zie je welke oefenreeksen passen bij capaciteitentests van LTP assessments. Dit zijn de tijdsgebonden tests.
LTP capaciteitentests |
Voorbereidingspakket voor LTP van 123test |
| LTP Abstracte figuren test | Oefenreeksen Abstracte figuren |
| LTP Abstracte matrix test | Oefenreeksen Matrices |
| LTP Numerieke inzicht test (LTP NIT) | Oefenreeksen Numeriek logisch redeneren |
| LTP Verbale relaties (verbale analogieën) | Oefenreeksen Verbale relaties (analogieën) |
| LTP Cijferreeksen test | Oefenreeksen Cijferreeksen |
| LTP Syllogismen test | Oefenreeksen Syllogismen |
| LTP Rekenvaardigheid | Oefenreeksen Rekenen |
LTP G-test |
Voorbereidingspakket voor LTP van 123test |
| LTP Figurenreeksen | Oefenreeksen [Figurenreeksen] |
| LTP Abstracte matrix test | Oefenreeksen Matrices |
| LTP Cijferreeksen test | Oefenreeksen Cijferreeksen |
| LTP cijferanalogieën | Oefenreeksen Hebbenweniet |
| LTP Patroonanalogieën | Oefenreeksen Hebbenweniet |
| LTP Patroon vouwen | Oefenreeksen [Kubussen] |
Het LTP Voorbereidingspakket
Cijferreeksen
Cijferreeksen
In een assessment zitten bijna altijd ook numerieke testen zoals Cijferreeksen, ook als de functie waarop je solliciteert weinig met getallen te maken heeft. Dit komt omdat je toekomstige werkgever inzicht wil krijgen in alle onderdelen van jouw intelligentie (abstract, verbaal en numeriek).
Bij Cijferreeksen gaat het om het herkennen van relaties tussen cijfers. Bij deze testen is het belangrijk dat je eenvoudig rekenen gewoon uit je hoofd kunt doen. Het gaat daarbij om optellen, aftrekken, delen en vermenigvuldigen. Het is zonde om hier veel tijd aan te verspillen want die wil je gebruiken om de relaties tussen de cijfers te vinden.
In zo’n relatie (of reeks) is een trend te zien die jou informatie geeft over het antwoord.
Cijferreeksen variaties
Het lastige aan cijferreeksen is dat er een aantal variaties zijn:
- optellen en aftrekken;
- vermenigvuldigen en delen;
- breuken, percentages, decimalen en machten;
- getallen overslaan;
- toenemende of afnemende veranderingen;
- reeks van berekeningen.
Daarnaast moet je de cijferreeksen vaak snel en zonder rekenmachine kunnen maken, daar hebben veel kandidaten moeite mee. Geen zorgen, cijferreeksen kun je namelijk goed oefenen. Hieronder illustreren we enkele voorbeelden van cijferreeksen, zodat je een goed beeld krijg van de cijfferreeksen ter voorbereiding op jouw assessment.
Cijferreeksen voorbeeld 1
2-4-6-8-10-?
Bij deze eenvoudige cijferreeks wordt telkens 2 opgeteld bij het vorige getal. In dit voorbeeld is het antwoord dus 12. Wanneer je deze cijferreeks in een grafiek zou zetten dan krijg je een rechte, stijgende lijn omdat telkens met hetzelfde getal wordt opgeteld. Wanneer je weet dat er sprake is van zo’n rechte, stijgende lijn, dan weet je bijvoorbeeld ook dat een cijfer dat lager is dan de laatste bekende uit de cijferreeks niet het correcte antwoord kan zijn.

Cijferreeksen voorbeeld 2
Een cijferreeks kan natuurlijk ook een andere richting hebben zoals bij het volgende voorbeeld:
144-134-124-114-104-94-?
Bij deze reeks krijg je het volgende getal door 10 af te trekken van het voorgaande getal. Het antwoord zou in dit geval 84 zijn (94 minus 10). Ook hier zie je weer een rechte lijn, maar nu eentje die daalt.

Bij rechte lijnen of reeksen gaat het altijd om optellen en aftrekken. Hierdoor zijn ze relatief makkelijk. Tenzij jouw hoofdrekenen natuurlijk ver onder de maat is.
Cijferreeksen voorbeeld 3
Er zijn ook ingewikkelder verbanden in de cijferreeksen verwerkt waarbij de stijging of daling niet gelijkmatig is maar juist exponentieel. Dit betekent dat getallen snel groter of juist kleiner worden. Vaak zijn zulke cijferreeksen al iets moeilijker omdat de rekensommen die je moet maken lastiger zijn.
Bekijk onderstaande cijferreeks om het exponentiële verband te begrijpen:
2-6-18-54-162-?
Het juiste antwoord is 486 want bij deze cijferreeks vermenigvuldig je steeds met 3. Je ziet in de grafiek duidelijk dat er een exponentiële stijging is. Vergeleken met rechte verbanden is de stijging of daling dan ook veel groter en daardoor wat lastiger te doorzien. Wanneer je een dalende, exponentiële trend ziet dan moet je delen i.p.v. vermenigvuldigen.

Cijferreeksen voorbeeld 4
Om het nog wat ingewikkelder te maken zijn er ook cijferreeksen waar de relaties tussen de cijfers elkaar afwisselen. Dus een recht en een exponentieel verband. Dan zijn er dus verschillende bewerkingen in één cijferreeks. Onderstaande cijferreeks is daar een voorbeeld van:
1-7-8-56-57-399-?
In dit geval heb je afwisselend een vermenigvuldiging en een optelling. De vermenigvuldiging is met 7 en dan wordt er 1 bij opgeteld. Deze twee bewerkingen herhalen zich. Het juiste antwoord is hier 400. Namelijk 399 plus 1. Bij deze cijferreeks merk je al dat het kennen van de tafels handig is want dat 7 x 8 = 56 moet je meteen weten.

De boogjesmethode
De verbanden die je ontdekt in de cijferreeksen kun je het beste met de boogjesmethode uitschrijven. Hierdoor maak je minder fouten en dwing je jezelf om volgens het verband te blijven rekenen. Wanneer je deze methode gebruikt dan twijfel je niet of je antwoord wel klopt. Je weet het gewoon.
Bij de cijferreeks hieronder zie je hoe de boogjesmethode werkt. Je ziet dat de cijferreeks omhoog loopt maar start met een 0. Hierdoor weet je zeker dat er geen vermenigvuldiging plaatsvindt bij de eerste stap, maar wat gebeurt er wel?

Je kunt beginnen met gewoon uitschrijven wat er gebeurt. Bijvoorbeeld dat er telkens 3 bij komen. Alleen bij de stap van 9 naar 15 gaat dat mis. Dus dit is niet wat er gebeurt. 3 x 2 = 6, maar ook dit helpt je niet verder. Bij sommige reeksen gaat de bewerking over meer dan één getal. Ook in dit geval gebeurt dat. 0 + 3 = 3. 3 + 3 = 6. Anders gezegd: het 3e getal is de som van twee voorgaande getallen. Het correcte antwoord = 24, want 9 + 15 = 24.
Ingewikkelde cijferreeksen oplossen met de boogjesmethode
Met de boogjemethode kun je cijferreeksen oplossen die je nooit zou oplossen als je niets opschrijft. Maak er dus een gewoonte van om een cijferreeks als een puzzel te zien waarbij je met ‘trial and error’ verschillende dingen probeert met de boogjesmethode. Hoe vaker je dit doet, des te sneller los je deze opgaven op.
Boogjesmethode voorbeeld 1
Bij onderstaande cijferreeks zal het wel even duren voor je ziet wat er gebeurt. Je ziet in elk geval al snel dat de reeks daalt. Dit gebeurt wel met aparte stappen. Je kunt eerst opschrijven wat er per stap gebeurt. Van 34 naar 21 betekent dat er 13 wordt afgetrokken. Van 21 naar 13 betekent dat er 8 wordt afgetrokken.

Wanneer je goed oplet dan zie je 13 en 8 ook terug in de cijferreeks. Wees alert op zulke hints want opeens kun je dan het verband gaan zien, zoals bij deze cijferreeks.
Boogjesmethode voorbeeld 2
Bij complexere cijferreeksen lopen er vaak twee verbanden door elkaar heen. Het is belangrijk dat je je hiervan bewust bent want vooral bij ‘onverklaarbare’ overgangen zijn er vaak twee onafhankelijke verbanden. Bij onderstaande cijferreeks is sprake van twee onafhankelijke verbanden.
 <
<
Bij de blauwe cijferreeks wordt er telkens 2 bij opgeteld. Dat is een eenvoudig verband, maar als je niet ziet dat er twee cijferreeksen zijn dan zul je dit niet snel door hebben. De zwarte cijferreeks is telkens een vermenigvuldiging met 3. Het goede antwoord is dus 81 (3 x 27). Als je de cijferreeks nog verder laat doorlopen dan komt na 81 natuurlijk 11 + 2.
Actief oefenen
Websites waar je tafels of andere makkelijke rekensommen kunt oefenen zijn heel handig om beter te worden in cijferreeksen. Hoe minder tijd je kwijt bent met rekenen, des te meer tijd heb je voor het ontdekken van de verbanden in de cijferreeks. Bovendien krijg je door te oefenen meer zelfvertrouwen doordat cijfers niet meer zo ‘bedreigend’ voor je zijn.
Wat je ook helpt is zélf cijferreeksen ontwerpen. Het leuke is dat je zelf kunt controleren of je een goede cijferreeks hebt bedacht want je kunt de reeks gewoon blijven verlengen.
Tips voor het oplossen van Cijferreeksen:
- Ga door naar een volgende opgave als je er niet uitkomt. Wanneer je te lang bij één opgave stil blijft staan dan verlies je tijd aan een opgave die je wel snel kunt oplossen.
- Gebruik de boogjesmethode om verbanden te herkennen.
- Maak aantekeningen bij cijferreeksen die je niet meteen begrijpt en beschrijf in je hoofd wat je doet. Door het onder woorden te brengen dwing je jezelf tot een constructieve aanpak. Dat bereik je niet door naar een opgave te blijven staren.
- Wanneer je de boogjesmethode gebruikt, schrijf dan ook op welke berekeningen je maakt, niet alleen de getallen. Anders vergeet je namelijk hoe een cijferreeks begon.
- Probeer het verband van de cijferreeks te doorzien (stijgend/dalend, recht/exponentieel/wisselend).
- Let op wanneer er grote en kleine stappen door elkaar lopen. Zijn er dan misschien twee verbanden?
- Achteraan de cijferreeks beginnen kan zinvol zijn omdat de grootte van de getallen laat zien welke bewerking er uitgevoerd wordt.
- Streep slim antwoorden weg. Cijferreeksen zijn meerkeuzevragen dus bepaalde antwoorden kun je wegstrepen als je het verband al weet. Hierdoor vergroot je jouw gokkans.
Oefening baart kunst!
Het is erg belangrijk om te oefenen voor een capaciteitentest.
Omdat cijferreeksen je numerieke intelligentie meten, word je hier ook beter in als je andere numerieke testen oefent.
Figuurreeksen
Figuurreeksen
Met Figuurreeksen test je hoe goed je logisch en abstract kunt redeneren. Bij deze test zie je een serie figuren. In de serie is er bij elke volgende figuur iets veranderd ten opzicht van de vorige. In deze veranderingen zit een verband dat jij moet ontdekken. Wanneer je dit verband hebt ontdekt kun je zelf de serie aanvullen met een volgende figuur.
Voorbeeldopgaven
Om je een idee te geven van hoe figuurreeksen eruit zien volgen hier een paar voorbeelden. Probeer eerst zelf te bedenken wat het antwoord moet zijn voordat je naar de uitleg onder de opgave kijkt.
Voorbeeld 1

Het goede antwoord bij deze figuurreeks is A. Als eerste draait de opening in het figuur steeds een kwart tegen de klok in. Daarnaast wijst het uitsteeksel steeds naar een positie in een diagram. Deze positie draait met de klok mee en slaat steeds twee stapjes over. Als laatste wordt de lijn van het figuur elk volgend figuur een stukje dikker.
Voorbeeld 2

Bij deze figuurreeks is B het goede antwoord. Elk plaatje is in evenwicht. In het eerste plaatje is te zien dat twee grijze blokjes op de eerste positie (rechts), vanuit het midden, gelijk staat aan één grijs blokje op de tweede positie vanuit het midden (links). In het tweede figuur is te zien dat twee grijze blokjes gelijk staan aan één rood blokje. Ook blijkt uit het verloop van de plaatjes dat het totale 'gewicht' van de blokjes per plaatje oploopt met 4 (2 per kant). Volgens deze regels is B de enige optie met de goede aantallen en een evenwicht.
Voorbeeld 3

Het goede antwoord bij deze laatste figuurreeks is C. Het patroon voor het plusteken is dat er bij elk volgend blokje een bij komt. Het patroon voor de cirkel is dat er bij een volgend blokje een bij komt, daarna een af gaat, en dit herhaalt zich. De driehoekjes zijn hier niet relevant maar bedoeld om je af te leiden.
Tips voor het oplossen van figuurreeksen
Let op de vorm van de figuren
Verandert de vorm van de figuur of blijft die gelijk in de volgende plaatjes? Als er meer dan één figuur te zien is, blijven de vormen allemaal gelijk of is er één die constant verandert?
Let op het aantal figuren
Blijft het aantal figuren gelijk in de volgende plaatjes? Wordt het aantal meer of minder, of zit er een ander wisselend patroon in?
Let op de plaats van de figuren
Verandert de figuur/figuren van plaats? Verandert misschien alleen één bepaald deel van een figuur van plaats? Kijk ook naar hoe de figuren verschuiven: met de klok mee, tegen de klok in, naar de tegenovergestelde hoek, naar de hoek ernaast. Misschien blijven ze één plaatje op dezelfde positie voordat ze weer verschuiven?
Let op kleur
Blijft de kleur van de figuur/figuren gelijk of verandert die in de volgende plaatjes? Verandert er maar één figuur steeds van kleur? Is één figuur constant dezelfde kleur?
Let op eventuele lijnen
Zijn er opvallende lijnen in het plaatje? Zo ja, verandert die? Als er zowel lijnen als figuren in het plaatje te vinden zijn, is er een patroon te vinden tussen de verandering in lijnen ten opzichte van eventuele veranderingen bij de figuren?
Probeer echt te beredeneren welke figuur moet volgen
Probeer goed je redeneringsvermogen te gebruiken om te voorspellen welk figuur in de reeks moet volgen. Ga niet direct alle plaatjes bekijken om één daarvan in de reeks te passen. Je moet echt kunnen beredeneren waarom die ene figuur in de reeks past.
Oefening baart kunst!
Bij elke capaciteitentest is het verhogen van je snelheid essentieel om een hogere score te halen. Het is daarom erg belangrijk om te oefenen.
Als je oefent kan je score hoger worden. Jouw kans op het krijgen van die felbegeerde baan wordt daarmee ook groter.
Oefen zoveel als je kunt. Dan kun je je opgaven sneller en efficiënter oplossen en krijg je een hogere score.
Omdat figuurreeksen je abstracte intelligentie meten, word je hier ook beter in als je andere abstracte testen oefent.
Analogieën
Analogieën
Met Analogieën test je je verbale intelligentie: hoe goed zie jij relaties tussen woorden?
Het is geen taaltest, al helpt het wel als je een goed taalgevoel en een grote woordenschat hebt.
Een test bestaat meestal uit 30 tot 40 opgaven.
Vooral bij analogieën is het belangrijk om steeds te blijven oefenen. Daarmee ontwikkel je namelijk je gevoel voor de verschillende soorten relaties die gebruikt worden in deze testen.
Wat is een analogie?
Een analogie is een relatie tussen woorden. Of anders gezegd: hoe verhouden de woorden zich tot elkaar? In de test moet jij die relatie (of: verhouding) gaan ontdekken. Als je de relatie hebt ontdekt weet je ook hoe je de oplossing kunt vinden.
Verhoudingen tussen woorden kun je een beetje vergelijken met rekensommen. Het kan je bij deze testen soms helpen om er een rekensom van te maken.
Voorbeelden van Analogieën
Voorbeeld 1: deel – geheel
Bos staat tot boom als kudde staat tot geit.
Voorbeeld 2: kruisen
Bij deze opgaven kun je woorden omwisselen of kruisen. Na het kruisen krijg je een andere analogie of verhouding, maar het is nog steeds logisch.
Stuur staat tot fiets als roer staat tot boot.
Door te kruisen, krijg je de volgende analogie:
Stuur staat tot roer als fiets staat tot boot.
Aan de linkerkant staan nu de stuurmiddelen en aan de rechterkant de vervoermiddelen. Bij zo’n kruising is het lastiger om de oplossing te vinden. Wanneer je nit snel de relatie ontdekt, kijk dan of je een kruising ziet.
Relaties die gebruikt worden bij analogieën
Tegenstellingen
Heet-koud; klein-groot; oud-nieuw; snel-langzaam.
Gradaties
Groter dan; kleiner dan; toename en afname; langer-korter; dikker-dunner; van weinig naar veel.
Deel/geheel
Bij deze relaties helpt het als je voor jezelf zinnen gebruikt om de vraag op te lossen (‘oplossingszinnen’). Bijvoorbeeld: ‘xx is een onderdeel van yy’ of ‘AA hoort bij BB’.
Synoniemen
Een andere term voor hetzelfde woord. Een grote woordenschat kan je vooral bij deze relaties erg helpen. Als je een woord niet kent dan is het namelijk erg lastig om de juiste relatie te achterhalen. Zoek daarom voortaan de betekenis op van woorden die je niet kent, ook al begrijp je ze ongeveer uit de context.
Functies
Wordt gebruikt door; wordt gemaakt door; wordt vervaardigd in; heeft als taak/ doel om.
Eigenschappen/kenmerken
De meest gebruikte zijn: hard-zacht; rond-vierkant; goed-slecht; glad-ruw; waardevol-goedkoop; massief-hol; scherp-bot.
Causale relaties
Wordt veroorzaakt door; is het gevolg van; leidt tot; is ontstaan uit.
Tips voor het oplossen van Analogieën
De oplossingszin
Gebruik een oplossingszin om de relatie te ontdekken. Bijvoorbeeld: ‘Zoals een schilder met een kwast een doek schildert, zo gebruikt een timmerman een hamer’.
Vermijd associatief redeneren
Hoe verleidelijk het ook is om woorden te koppelen die in het dagelijks leven goed bij elkaar passen (appel en sap), het gaat om de relatie tussen woorden.
Vergeet de kruising niet
Een gekruiste analogie is lastig te ontdekken omdat de relaties niet makkelijk te herkennen zijn. Ook helpt hierbij de oplossingszin niet.
Maak gebruik van de grammatica
Als je links en rechts dezelfde relatie moet vinden, kijk dan ook eens naar de grammatica. Vaak worden bij een analogie werkwoorden en zelfstandige naamwoorden gebruikt.
Zorg dat je alle relaties kent
Behalve de relaties die op deze pagina genoemd zijn, zijn er nog meer. Leer ze allemaal uit je hoofd. Schrijf ze op en leg ze op je bureau. Hoe sneller je de relaties ziet, des te beter. Zo houd je meer tijd over voor de moeilijkste analogieën.
Verander je perspectief
Doordat de analogie als een zin wordt weer gegeven gaat je brein er al snel heel creatief een logische zin van maken. Hierdoor verlies je uit het oog dat het alleen om de relatie tussen woorden gaat. Kijk daarom vanuit een ander perspectief naar de zin.
Oefening baart kunst!
Bij elke capaciteitentest is het verhogen van je snelheid essentieel om een hogere score te halen. Als je minder tijd kwijt bent aan de standaard relaties tussen woorden, dan heb je meer tijd om de lastige opgaven te beantwoorden. Het is daarom erg belangrijk om te oefenen.
Als je oefent kan je score hoger worden. Jouw jouw kans op het krijgen van die felbegeerde baan wordt daarmee ook groter.
Omdat analogieën je verbale intelligentie meten, word je hier ook beter in als je andere verbale testen oefent.
Syllogismen
Syllogismen
Een subtest die je tegen kunt komen bij het maken van een capaciteitentest is het syllogisme. Het syllogisme bestaat uit een tweetal stellingen die met elkaar samenhangen en waaruit je een conclusie kunt trekken. De vraag is welke conclusie de juiste is. Het syllogisme doet een sterk beroep op het vermogen tot verbaal en logisch redeneren. De syllogismentest duurt niet lang, meestal zijn het twintig opgaven die in je in acht minuten moet doen.
Bij syllogismen zitten, impliciet of expliciet, in de uitspraken bijna altijd drie gradaties:
- Het kan zijn dat iets zich altijd voordoet, het is in alle gevallen zo en het betreft alles.
- De tweede optie geeft aan dat het in geen van de gevallen zo is, niets is zo, het is nooit zo.
- Ten slotte is er een vage tussencategorie die het hele gebied tussen alles en niets bestrijkt: in sommige gevallen is het zo, soms of vaak, veel of weinig.
Voor zover deze gradaties impliciet zijn aangegeven, moet je ze expliciet maken, dat schept meer helderheid. Voor het oplossen is echter meer nodig.
Voorbeeld opgave Een syllogisme-opgave ziet er ongeveer zo uit: Stelling 1: Sommige houten dingen zijn ladders Stelling 2: Alle stalen gereedschappen zijn houten dingen. A: Alle stalen gereedschappen zijn ladders. B: Alle ladders die houten dingen zijn, zijn ook stalen gereedschappen. C: Er zijn ladders die geen stalen gereedschap zijn.
Syllogismen bezitten een uitwendige logica die kan afwijken van de werkelijkheid van alledag. Zo staat de tweede uitspraak over stalen gereedschappen op gespannen voet met de werkelijkheid, dit zijn immers nooit houten dingen, maar het gaat bij een syllogisme niet om de werkelijkheid maar om de logica.
Wat erg behulpzaam is bij syllogismen van het type ‘sommige/alle/geen’, is het visualiseren van de twee uitspraken door op je blocnote cirkeldiagrammen, de zogeheten Venn diagrammen, te tekenen.

Venn diagrammen zijn de meest gebruikte methode voor het oplossen van syllogismen. Een Venn diagram is een grafische voorstelling van alle mogelijke, hypothetische logische relaties tussen een eindige verzameling van beweringen. Door middel van de overlap tussen sommige beweringen kunnen conclusies getrokken worden uit de genoemde stellingen.
In het voorbeeld is antwoord C juist. Sommige ladders zijn geen houten dingen, dus de ladders en houten dingen hebben beperkte overlap. Daarnaast zijn alle stalen gereedschappen houten dingen, dus de cirkel van de stalen gereedschappen bevindt zich volledig in de cirkel van de houten dingen. Zoals je ziet is er ook een beperkte overlap met de ladders.
Als je nu de cirkels bekijkt en de beweringen ernaast legt kan je de volgende conclusies trekken:
- Je ziet in één oogopslag dat antwoord A onjuist is; sommige stalen gereedschappen zijn ook houten dingen, dus niet alle stalen gereedschappen zijn ladders.
- Antwoord B is ook onjuist, want deze conclusie kunnen we niet automatisch trekken. We weten niet zeker of de ladders (de rode cirkel) die overlappen met de houten dingen (blauwe cirkel) en stalen gereedschappen (groene cirkel) ook daadwerkelijk de stalen gereedschappen zijn; voor hetzelfde geld zijn deze ladders allemaal houten dingen.
- Antwoord C is wel juist; de cirkel van de ladder heeft voor een groot gedeelte geen overlap met de stalen gereedschappen; er zijn dus ladders die geen stalen gereedschap zijn.
Syllogismen oplossen aan de hand van Venn diagrammen
Hieronder volgen een aantal verschillende soorten opgaven met daarbij de oplossing weergegeven door middel van een Venn diagram. Bestudeer de opgaven en de Venn diagrammen goed; de meeste opgaven zijn op te lossen aan de hand van deze structuur. Aan het einde van de voorbeeldopgaven vind je de bijbehorende antwoorden
Opgave 1 Stelling 1: Sommige arbeiders zijn geen hardwerkende boeren. Stelling 2: Alle gepensioneerde artsen zijn hardwerkende boeren.
- A. Alle gepensioneerde artsen zijn arbeiders.
- B. Sommige arbeiders zijn geen gepensioneerde artsen.
- C. Sommige arbeiders zijn gepensioneerde artsen.

Opgave 2 Stelling 1: Alle kikkers zijn blauwachtigen. Stelling 2: Alle kikkers zijn giftigen.
- A. In ieder geval een deel van de giftigen zijn blauwachtigen.
- B. In ieder geval een deel van de giftigen zijn geen kikkers.
- C. In ieder geval een deel van de kikkers zijn blauwachtigen.

Opgave 3 Stelling1: Alle groenteboeren zijn alleenstaand. Stelling 2: Geen van de groenteboeren zijn miljonair.
- A. Geen van de antwoorden is een juiste conclusie.
- B. Geen van de miljonairs zijn alleenstaand.
- C. Alle groenteboeren zijn miljonair.

Opgave 4 Stelling1: Geen van de gestreepte paarden zijn kleine pony’s. Stelling 2: Alle zebra’s zijn gestreepte paarden.
- A. Geen van de zebra’s zijn kleine pony’s.
- B. Alle gestreepte paarden zijn kleine pony’s.
- C. Alle gestreepte paarden zijn zebra’s.

Opgave 5 Stelling1: Geen van de zevens zijn zessen. Stelling 2: In ieder geval een deel van de enen zijn zevens.
- A. In ieder geval een deel van de enen zijn zessen.
- B. In ieder geval een deel van de enen zijn niet zessen.
- C. Alle enen zijn zessen.

De antwoorden:
- 1. B
- 2. A
- 3. A
- 4. A
- 5. B
Omdat syllogismen je verbale intelligentie meten, word je hier ook beter in als je andere verbale testen oefent.
Matrices
Matrices
Met matrices test je je intellectuele en logische denkvermogen. Het lijkt alsof deze testen niets te maken hebben met de inhoud van de baan waar je naar solliciteert. Toch zijn ze heel geschikt om te testen hoe goed jij oplossingen kunt bedenken en of jij flexibel kunt omgaan met nieuwe informatie. De reden is dat jouw opleiding, ervaring of achtergrond bij abstracte testen geen invloed hebben op je resultaat. Daardoor kunnen ze je toekomstige ontwikkeling goed voorspellen. In je assessment zitten daarom bijna altijd abstracte testen zoals bijvoorbeeld matrices.
Hoe zien matrices eruit?
Elke matrix bestaat uit 17 figuren: de opgave zelf bestaat uit 9 figuren en je kunt kiezen uit 8 mogelijke antwoorden (A t/m H). Bij een matrix kun je op 3 manieren regels toepassen om het antwoord te vinden:
- Dezelfde regel geldt zowel horizontaal als verticaal.
- Er geldt horizontaal een bepaalde regel en er geldt verticaal een andere regel.
- De matrix is een doorlopende reeks van vakje 1 t/m vakje 9.
Voorbeeld 1

In bovenstaand voorbeeld wordt er zowel verticaal als horizontaal 1 regel toegepast. Zie het voorbeeld hieronder. Als je vakje 2 over vakje 3 schuift krijg je vakje 1 (horizontaal). Als je vakje 4 over vakje 5 schuift krijg je ook vakje 1. Dit geldt voor alle horizontale en verticale rijen. Het juiste antwoord (vakje 9) is: vakje 6 + vakje 9 = vakje 3 en vakje 8 + vakje 9 = vakje 7. Dus in vakje 9 past antwoord H.
Voorbeeld 2

Bij dit voorbeeld geldt er horizontaal een bepaalde regel en geldt er verticaal een andere regel.
- Horizontaal verschilt de vorm wat betreft het aantal hoeken: vakjes 1, 4 en 7 hebben per lijn 2 hoeken, vakjes 2, 5 en 8 hebben per lijn 0 hoeken, vakjes 3, 6 en 9 hebben per lijn 1 hoek.
- Verticaal verschilt de vorm wat betreft de raakvlakken van de figuren. De lijnen schuiven als het ware over elkaar heen. Vakjes 1, 2 en 3 raken elkaar alleen in het midden en overlappen nog niet. Vakjes 4, 5 en 6 raken elkaar op 2 punten. De twee lijnen zijn nog redelijk dicht bij elkaar. Vakjes 7, 8 en 9 raken elkaar ook op 2 punten maar er zit meer ruimte tussen de 2 lijnen.
Bij deze opgave geldt ook nog een andere regel die in alle vakjes gelijk is: alle figuren hebben 1 dikke en 1 dunne lijn. De dikke lijn schuift steeds verder naar boven, de dunne lijn schuift steeds verder naar beneden. Het juiste antwoord is daarom C.
Tips voor het oplossen van matrices
Matrices kunnen dus zowel verschillen in de hoofdregels (horizontaal/verticaal dezelfde regel, horizontaal/verticaal aparte regel, doorlopende reeks) als in overeenkomsten. Er zijn dus veel dingen waar je op moet letten. Zelf een paar matrices bedenken zou dus een goede oefening zijn: zo leer je creatief denken en de figuren op een abstracter niveau bekijken.
Regels en overeenkomsten die gebruikt worden bij matrices
- Kleuren. Welke kleurenpatronen komen voor per regel?
- Het aantal elementen per figuur plus het aantal elementen per rij.
- Iedere regel bevat bepaalde vormen.
- Optellen of aftrekken. Vakje 1 + Vakje 2 = Vakje 3. Of: Vakje 1 – Vakje 2 = Vakje 3.
- Reeksen. Wordt een regel bijvoorbeeld steeds uitgebreider? Dus: wordt een element steeds groter?
- De richting van een figuur. Wijst een lijn bijvoorbeeld altijd naar de linkerhoek of naar beneden?
- Het zwaartepunt van een figuur. Elementen binnen een figuur kunnen naar één bepaalde kant toe trekken per verticale of horizontale regel.
- Overlappingen, bijvoorbeeld in kleur. Bijvoorbeeld: blauw + groen = rood, paars + oranje = geel.
- Rekensommen. Het aantal elementen boven in een figuur kan bijvoorbeeld opgeteld worden bij of afgetrokken worden van het aantal elementen onder in een figuur.
- Onderlinge verhouding. Lopen lijnen parallel aan elkaar of kruisen ze elkaar juist?
- Patronen. Draait of verschuift een figuur binnen een regel?
Probeer deze kenmerken goed te onthouden: hoe meer regels/overeenkomsten je kent, hoe makkelijker het is om matrices snel te doorzien.
Voorbeeld 3
In dit voorbeeld gaan we het lijstje met kenmerken toepassen.
- Ieder figuur heeft gele sterren (kleuren, vormen).
- Ieder figuur heeft 1 kronkelende middenlijn, 2 schuine lijntjes en 1 verticaal lijntje (vormen).
- Het aantal sterren boven en onder de lijn is ongelijk, zowel in de horizontale als verticale serie. Dit kenmerk (aantal elementen) kunnen we dus vergeten.
- Optellen en aftrekken kan hier wel. Als we de sterren boven de lijn zien als PLUS en de sterren onder de lijn als MIN kunnen we rekensommen maken. Sterren vakje 1 = +2, sterren vakje 4 = +1, sterren vakje 7 = + 3. Vakje 1 + vakje 4 = vakje 7. Ter controle: Sterren vakje 1 = + 2, sterren vakje 2 = -4, sterren vakje 3 = -2. Vakje 1 + vakje 2 = vakje 3, namelijk 2-4 = -2.
- Het laatste dat opvalt is dat er binnen een bepaalde rij, zowel horizontaal als verticaal, patronen zijn waar het gaat om de lijntjes. Ieder lijntje bevindt zich per rij in een andere hoek. Daarnaast blijft de linkerhoek in een figuur altijd leeg.
Oefening baart kunst!
Bij elke capaciteitentest is het verhogen van je snelheid essentieel om een hogere score te halen. Het is daarom erg belangrijk om te oefenen.
Als je oefent kan je score hoger worden. Jouw kans op het krijgen van die felbegeerde baan wordt daarmee ook groter.
Oefen zoveel als je kunt. Dan kun je je opgaven sneller en efficiënter oplossen en krijg je een hogere score.
Omdat matrices je abstracte intelligentie meten, word je hier ook beter in als je andere abstracte testen oefent.
Figuren (overeenkomsten)
Figuren
Met Figuren test je hoe goed je hoofd- en bijzaken kunt scheiden. Het zijn abstracte testen die bijna altijd deel uitmaken van je assessment. Het voordeel van zulke abstracte testen is dat taalachterstanden niet uitmaken. Figuren bestaan eigenlijk uit een serie figuren. Het aantal figuren kan per opgave verschillen.
Bij de volgende voorbeelden bestaat de serie uit 10 figuren. De eerste 4 figuren zijn de opgave. Ze hebben maar één gemeenschappelijk kenmerk. Jij moet uitzoeken welke 2 van de onderste 6 figuren (de antwoorden) passen bij de bovenste 4 figuren. Dat ze passen betekent dat ze ook dat ene kenmerk gemeenschappelijk hebben.
Drie voorbeelden
In het voorbeeldplaatje hieronder zie je dat de bovenste 4 figuren allemaal vierkant zijn. Van de onderste 6 figuren zijn alleen (a) en (f) ook vierkant. Dat is dus het gemeenschappelijke kenmerk. De oplossing zit hier dus in de vorm van de figuren.
Probeer ook de voorbeelden 2 en 3 te maken. Kijk eerst naar de bovenste 4 figuren. Ga na wat ze gemeenschappelijk hebben. Probeer nu de TWEE andere figuren te vinden uit de onderste 6 die dat ook hebben.

Uitleg voorbeeld 2
De bovenste 4 figuren zijn allemaal op dezelfde manier gearceerd. Dit is ook zo bij (b) en (e). De andere figuren zijn donkerder dan de bovenste 4 figuren dus die passen er niet bij.
Uitleg voorbeeld 3
De bovenste 4 figuren bestaan allemaal uit een ronde/ovale vorm waarbij een rechte lijn de cirkel/het ovaal schampt. De lijn snijdt de cirkel/het ovaal niet. Bij (c) en (f) is dat ook zo. Dat zijn dus ook de goede antwoorden.
Voorbeeld 4
Als je zoekt naar overeenkomsten dan zie je bij onderstaande opgave het volgende in de bovenste 4 vakjes:

1. Een vijfpuntige ster, qua vorm en kleur hetzelfde.
2. Een vijfpuntige ster, qua grootte verschillend.
3. Een vijfpuntige ster, op verschillende locaties.
4. Elke ster heeft twee lijnen in het vakje staan.
5. Elke ster heeft twee even lange lijnen in het vakje staan.
6. Elke ster heeft lijnen die evenwijdig aan elkaar zijn (ze kruisen nooit).
7. De twee lijnen raken of kruisen de ster altijd.
Deze conclusies leiden je naar de twee goede antwoorden. Als je de regels goed in je hoofd hebt weet je ook waarom de andere opties niet juist zijn.
- Antwoord A is niet goed, omdat het niet voldoet aan overeenkomst 5 en 7.
- Antwoord B is niet goed omdat het niet voldoet aan overeenkomst 7.
- Antwoord C is niet goed omdat het niet voldoet aan overeenkomst 7.
- Antwoord D is niet goed omdat het niet voldoet aan overeenkomst 5.
E en F zijn daarom de goede antwoorden. Deze test zou ook met heel veel andere varianten gemaakt kunnen worden, bijvoorbeeld door met de vorm van de ster te variëren.
Tips voor het oplossen van Figuren
Zoals je in de voorbeelden kunt zien zijn er heel veel kenmerken die de figuren gemeenschappelijk kunnen hebben. Met een beetje creativiteit zijn er veel gemeenschappelijkheden voor figuren te bedenken. Een goede oefening is dan ook om zelf een figurenopgave te bedenken.
Hieronder staan kenmerken van figuren waar je naar op zoek kunt gaan. Zo kun je snel de juiste antwoorden vinden. Bekijk ze goed, zo weet je sneller naar welke overeenkomsten tussen figuren je kunt zoeken.
Kenmerken van figuren:
- Vormen
- Onderlinge verhouding: lopen lijnen parallel aan elkaar of kruisen ze elkaar juist?
- Aantal figuren/lijnen/elementen.
- Dominantie: sommige figuren maken een ander figuur onzichtbaar.
- Gesloten en open figuren. Kijk bij open figuren waar de opening zit
- Kleuren en arcering: is het echt gelijk aan elkaar of lijkt dat maar zo?
- Even en oneven, bijvoorbeeld de punten van een ster.
- Lengte van figuren.
- Plaats in het vakje: allemaal in het midden of juist rechtsboven of nog ergens anders?
- Hoeken van figuren: hebben ze juist wel of juist niet een rechte hoek (90 graden)?
- Sommige ingewikkelde figuren worden alleen maar een aantal graden gedraaid, maar blijven verder precies hetzelfde. Kijk goed naar unieke kenmerken van complexe figuren.
- Doorgetrokken of onderbroken lijnen.
- Afmetingen: grote of kleine figuren.
- Rechte, scherpe of stompe hoeken.
- Wel of geen rondingen in de figuren.
Een belangrijke fout die je bij deze test kunt maken is het zoeken naar een bepaalde beweging of volgorde. Bij een cijferreeks gaat het wel om die volgorde, maar bij Figuren gaat het om een overeenkomst. Uitdaging is om door de bomen het bos te blijven zien. Door bekend te raken met bovenstaande mogelijkheden voor overeenkomst ben je minder gevoelig voor ruis en misleidende figuren die nietszeggend zijn.
Numeriek inzicht (tabellen en grafieken)
Numeriek inzicht
Bij je assessment zitten bijna altijd Numerieke testen, ook als je functie weinig met getallen te maken heeft. Dit komt omdat je toekomstige werkgever inzicht wil krijgen in alle onderdelen van jouw intelligentie (abstract, verbaal en numeriek). Wel is het zo dat voor bijvoorbeeld een juridische functie je score op numeriek inzicht minder zwaar weegt. Toch is voor elke functie deze test belangrijk. Wanneer werkgevers de luxe hebben om streng te selecteren, laten ze soms alleen kandidaten door die op alle onderdelen bovengemiddeld scoren. Het is dus erg belangrijk om je rekenvaardigheid op te halen zodat je gevoel voor cijfers groeit.
Hoe ziet een numerieke test eruit?
Bij de testen voor numeriek inzicht krijg je tabellen of grafieken voorgeschoteld. Om de vraag te beantwoorden moet je informatie uit die tabellen of grafieken halen.
- Soms kun je het antwoord direct aflezen uit de tabellen of grafieken.
- Soms moet je eerst één of meer berekeningen uitvoeren voordat je jouw antwoord kunt geven.
Alle vragen hebben maar één goed antwoord. Maar let op: soms is het antwoord niet te bepalen als de gegevens niet toereikend zijn. Realiseer je bij het maken van de opgaven het volgende:
- De informatie in de tabellen en grafieken is fictief.
- Het gaat er alleen om of je de gegeven informatie goed verwerkt en of je de benodigde berekeningen kunt maken.
Laat je dus niet in de war brengen doordat een antwoord niet logisch of realistisch is. In een opgave kan het goede antwoord best zijn dat apen intelligenter zijn dan mensen. Het gaat om je inzicht in cijfers.
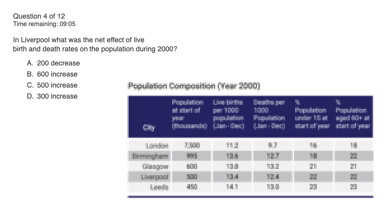
Voorbeeld van een numerieke test

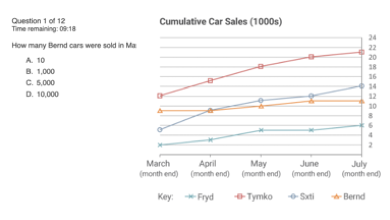
In deze opgave zie je een tabel met een titel. De titel is erg belangrijk omdat hier precies staat wat je in de tabel kunt zien. Dankzij de titel weet je dus ook welke conclusie je wel of niet mag trekken. De vraag is: Bij welk land is de procentuele toename van de vraag naar frisdranken het grootst wanneer 2013 vergeleken wordt met 2009? Elke opgave begint met goed lezen. Wat willen ze precies weten? In dit geval gaat het om de grootste procentuele stijging over 2009 en 2013 binnen één land. Wat er in de tussenliggende jaren gebeurt is hier dus niet relevant.
- A. Duitsland
- B. Frankrijk
- C. Nederland
- D. Spanje
Om deze opgave te maken moet je het rekenen naar procenten dus opfrissen. Gebruik een rekenmachine en kladpapier. Het juiste antwoord is C,. Nederland. Frankrijk valt direct af, want zowel in 2009 als in 2013 is de vraag naar frisdrank exact hetzelfde; er was geen stijging. In Spanje is wel een stijging te zien van 25.000 liter en in Duitsland is er zelfs een stijging van 100.000 liter te zien. Nederland heeft weliswaar een stijging van 15.000 liter, maar dit is relatief gezien wel de grootste toename, namelijk ongeveer 23%. Op het eerste gezicht kiezen veel mensen voor Duitsland, omdat hier de absolute vraag naar frisdranken het grootst is. Maar omdat er al een grote vraag is (in 2009 al 600.000 liter) is de procentuele stijging veel kleiner dan in Nederland, namelijk maar zo’n 14%. Ken je de formule nog? (nieuw- oud)/ oud * 100
Tips voor het oplossen van Numerieke testen
- Besteed niet te veel tijd aan één vraag als je geen idee hebt hoe je tot het antwoord moet komen.
- Zorg dat je de tafels van 1 tot 15 uit je hoofd kent; hierdoor zal je sneller gevoel krijgen voor het juiste antwoord.
- Herhaal basiswiskunde zoals het rekenen met procenten.
- Raak vertrouwd met je rekenmachine zodat je sneller kunt werken.
- Check elke keer of je ook echt antwoord geeft op wat er precies wordt gevraagd.
- Probeer zelf een numerieke test te bedenken, daardoor vergroot je je inzicht in dit soort testen.
- Wanneer je een grafiek te zien krijgt, kijk dan goed naar de x- en de y-as zodat je weet wat je op de grafiek staat.
- De titel van grafieken of tabellen is belangrijk om snelheidsfouten te voorkomen.
- Houd je bij het trekken van conclusies altijd aan de informatie die in de opgave gegeven wordt.
- Streep antwoorden weg als je deze antwoorden kunt uitsluiten.
- Blijf rustig als de vraag je in eerste instantie niet helder is. Lees het nog een keer en vat de vraag voor jezelf samen.
- Google op de termen absoluut en relatief, want ze worden veel gebruikt bij deze opgaven.
- Bereken vooraf hoeveel tijd je hebt per opgave.
- Een correct antwoord hoeft niet altijd overeen te komen met de werkelijkheid.
- Bekijk elke opgave als een uitdagende puzzel in plaats van iets waar je toch nooit uit komt.
- Kijk bij complexe grafieken ook naar de algehele trend.
- Wanneer je nog maar weinig tijd hebt, kies dan voor een beredeneerde gok in plaats van geen antwoord te geven.
Oefening baart kunst!
Het is erg belangrijk om te oefenen voor een capaciteitentest.
Als je oefent kan je score hoger worden. Jouw jouw kans op het krijgen van die felbegeerde baan wordt daarmee ook groter.
Oefen zoveel als je kunt. Dan kun je je opgaven sneller en efficiënter oplossen en krijg je een hogere score.
Verbaal redeneren
Verbaal redeneren
Met Verbaal Redeneren test je je redeneervermogen. Verbaal redeneren is het begrijpen, analyseren en interpreteren van (in dit geval) geschreven informatie. Deze test laat zien hoe goed je verbale informatie kunt opnemen, verwerken en gebruiken om relevante vragen of stellingen te beantwoorden. Het geeft informatie over het werkniveau dat een werkgever van je kan verwachten. Eigenlijk is verbaal redeneren een ‘volwassen’ vorm van begrijpend lezen. Daarnaast is het een skill die wij vaak gebruiken in ons dagelijks leven en daarom is het erg nuttig om dit te trainen.
Stellingen beoordelen
Vragen in deze test bestaan uit stukjes tekst plus stellingen over die tekst. Als je de tekst goed leest weet je of de stelling waar of niet waar is of niet te bepalen op basis van de tekst. Een stelling is waar als deze klopt met de informatie in de tekst. Een stelling is niet waar als deze niet klopt met de informatie in de tekst. Een stelling is niet te bepalen op basis van de tekst als je uit de tekst niet kunt opmaken of deze waar of onwaar is; je hebt extra informatie nodig om dat te kunnen bepalen.
Voorbeeld
Het komt wel eens voor dat er ’s nachts geen maan aan de hemel staat, en het tóch helder genoeg is om buiten een boek te lezen of objecten op honderden meters afstand te zien. Volgens onderzoekers zijn zulke opvallend lichte nachten niet gerelateerd aan de maan, maar het gevolg van atmosferische golven, verstoringen in de atmosfeer waarbij lucht met verschillende eigenschappen elkaar tegenkomt. Als zich meerdere van die atmosferische golven in de buurt van elkaar bevinden kan dat ervoor zorgen dat de gloed in de atmosfeer of ‘airglow’, die altijd in meer of mindere mate in de atmosfeer aanwezig is, tijdelijk tot tien keer zo sterk kan worden. Stelling: Door ‘airglow’ kan een maanloze nacht net zo licht zijn als een heldere nacht met maanlicht. Antwoord: Waar / Niet waar / Niet te bepalen op basis van de tekst Uitleg: Deze stelling is niet te bepalen op basis van de tekst omdat er geen vergelijking wordt gemaakt tussen maanlicht en ‘airglow’ sterkte.
Tips voor het oplossen van opgaven voor Verbaal Redeneren
Lees eerst de tekst
Het kan verleidelijk zijn om eerst de stelling te lezen en daarna in de tekst te zoeken naar een relevant woord of een relevante zin. Maar zo kun je informatie missen die op het eerste gezicht niet belangrijk lijkt te zijn voor de stelling, maar dat later toch wel blijkt te zijn. Het is beter om eerst de tekst helemaal te lezen voordat je de stelling bekijkt. Zo lees je alle informatie in de tekst onbevooroordeeld, zonder dat je zoekt naar bepaalde woorden of zinnen.
Wees je ervan bewust van hoe de tekst in elkaar zit
In een goedlopende tekst staan zinnen niet kriskras door elkaar maar hebben ze een relatie tot elkaar. Een tekst als geheel heeft een bepaalde gedachte maar ook elke zin heeft nuances en kleine details die belangrijk kunnen zijn. De stellingen gaan niet altijd over hetzelfde onderdeel van de tekst. Soms gaat deze over de algemene conclusie die je uit de tekst als geheel kunt trekken. Een andere keer gaat deze over de relatie tussen een aantal zinnen of zinsdelen in de tekst. Zelfs komt het voor dat een stelling gaat over maar één bepaald detail of nuance in een zin. Probeer daarom bij het lezen van de stelling jezelf af te vragen over welk deel van de tekst deze gaat.
Gebruik ALLEEN de tekst
De stellingen gaan altijd alleen maar over de informatie in de tekst. Het kan soms verleidelijk zijn om er zelf dingen bij te gaan bedenken. Zeker als de tekst over een onderwerp gaat waar jij veel vanaf weet, of laatst nog wat over hebt gelezen. Focus je op wat er precies in de tekst staat en vergeet wat jij er allemaal nog meer over weet. Wees daarom ook niet bang om te kiezen voor de optie ‘niet te bepalen op basis van de tekst’.
Oefening baart kunst!
Omdat analogieën je verbale intelligentie meten, word je hier ook beter in als je andere verbale testen oefent.
Watson Glaser (Kritisch redeneren)
Watson Glaser
De test Watson-Glaser test hoe goed je bent in verbaal kritisch denken. Deze test bestaat uit verschillende categorieën:
- Conclusies
- Aannames
- Interpretaties
- Deducties
- Evaluaties
Conclusies
Conclusies zijn gevolgtrekkingen die je logischerwijs uit de gegeven informatie kunt trekken. In deze categorie is het aan jou om te bepalen of de gegeven conclusie juist of onjuist is en in welke mate. Dit beoordeel je aan de hand van een klein stukje tekst waar de conclusie vervolgens betrekking op heeft.
Een Conclusieopgave ziet er vaak zo uit:
Hoewel het in Nederland nog klinkt als toekomstmuziek, wordt het in de Verenigde Staten nu werkelijkheid. Een Amerikaans tech-bedrijf gaat microchips implanteren bij zijn werknemers. Hiermee kan het personeel betalen in de bedrijfskantine, deuren openen, inloggen op computers en het kopieerapparaat bedienen.
Het softwarebedrijf Three Square Market uit de staat Wisconsin zegt met dit project het eerste bedrijf in de Verenigde Staten te zijn dat aan al zijn werknemers de optie biedt om een chip te laten implanteren.
Men gaat het kleinnood tussen de duim en wijsvinger plaatsen. Er wordt gebruik gemaakt van zogeheten NFC-technologie. Deze technologie gebruikt men ook in chipkaarten en bankpassen met contactloos betalen.
Over eventuele nadelige gevolgen voor de privacy zijn de meningen verdeeld. Volgens sommige deskundigen heeft zo’n kleine chip maar maximaal 10 centimeter bereik. Dat zou het voor kwaadwillenden onmogelijk maken om gebruikers vanaf een afstand te volgen. Anderen waarschuwen dat chipdragers weliswaar niet op de centimeter nauwkeurig getraceerd kunnen worden, maar wel op enkele tientallen meters.
Conclusie: Wanneer de chip geïmplanteerd is, valt hij niet te traceren. Antwoordmogelijkheden: Waar – Waarschijnlijk waar – Meer informatie nodig – Waarschijnlijk onwaar – Onwaar Het goede antwoord bij deze opgave is ‘onwaar’. Volgens de tekst kan men de chip op enkele tientallen meters traceren. Daarom is deze conclusie onwaar.
Aannames
Een aanname is iets dat je als vanzelfsprekend beschouwt, op basis van de beschikbare informatie. In tegenstelling tot conclusies zijn aannames beweringen die je als correct aanneemt, juist door de afwezigheid van bewijs. Het doel in deze opgaven is om op basis van een klein stukje tekst en een gegeven aantal aannames, voor elke aanname te bepalen of deze wel of niet gedaan wordt in de tekst.
Een Aannameopgave ziet er vaak zo uit:
Google gaat webuitgevers actief waarschuwen als hun websites advertenties bevatten die als irritant worden ervaren. De browser Chrome van Google gaat vanaf volgend jaar reclames blokkeren die nieuwe richtlijnen overtreden.
Aanname: De richtlijnen voor website advertenties zijn of worden vernieuwd. Antwoordopties: Aanname is gedaan – Aanname is niet gedaan Het goede antwoord bij deze voorbeeldopgave is ‘aanname is gedaan’. De tekst spreekt over nieuwe richtlijnen. Als je nieuwe richtlijnen maakt, moet je eerst oude richtlijnen vernieuwen.
Interpretaties
Bij interpretaties wordt gekeken naar hoe je informatie verwerkt en of je dit correct interpreteert, gebaseerd op deze informatie. Je moet bij een interpretatie beoordelen of een conclusies wel of niet logisch voortkomt uit de gegeven tekst. Je geeft dit aan door bij elke conclusie te kiezen of deze juist of onjuist is.
Een Interpretatieopgave ziet er vaak zo uit:
Albert Heijn is door dierenwelzijnsorganisatie Wakker Dier tot Liegebeest van 2017 verkozen. De supermarktketen plaatste in maart een foto van varkens in de wei bij een Allerhande-artikel over de AH Excellent Serranoham. Volgens Dierenwelzijnsorganisatie Wakker Dier zitten de Spaanse serranohamvarkens in werkelijkheid hun hele leven in een krap hok zonder stro. In de toekomst zal Albert Heijn de foto dan ook niet meer gebruiken bij artikelen of reclames over Serranoham.
Interpretatie: De foto van de serranohamvarkens is waarheidsgetrouw. Antwoordopties: Conclusie volgt (uit de tekst) – Conclusie volgt niet (uit de tekst) Het goede antwoord op deze voorbeeldvraag is ‘conclusie volgt niet’. Volgens Wakker Dier klopt de foto van de serranohamvarkens niet met de situatie waarin de varkens daadwerkelijk leven. Daarom volgt deze conclusie niet logischerwijs uit de tekst.
Deducties
Bij deducties krijg je een stelling en een conclusie. Je moet bepalen of de conclusie wel of niet logisch volgt uit de stelling.
Een Deductieopgave ziet er vaak zo uit:
De NS en de gemeente Amsterdam stappen over naar een genderneutraal taalgebruik. Het Amsterdamse vervoersbedrijf GVB, Schiphol en goededoelenorganisatie Hivos maken al langer gebruik van het neutrale ‘uw attentie alstublieft’, ‘beste reizigers’ of ‘beste donateur’.
Deductie: De gemeente Amsterdam heeft veel klachten ontvangen over het gebrek aan genderneutraal taalgebruik. Antwoordopties: Conclusie volgt – Conclusie volgt niet Het goede antwoord op deze voorbeeldvraag is ‘conclusie volgt niet’. De stelling geeft geen informatie over de reden voor de switch naar genderneutraal taalgebruik. Daarom volgt deze conclusie niet logischerwijs uit de tekst.
Evaluaties
Bij het onderdeel evaluaties moet je onderscheid maken tussen zwakke en sterke argumenten die worden gegeven op basis van één of meer stellingen/vragen. Argumenten zijn beweringen die worden gebruikt om een stelling te onderbouwen of juist te ontkrachten. Een sterk argument is belangrijk en direct gerelateerd aan de stelling. Een zwak argument is minder of helemaal niet gerelateerd aan de stelling. Daarnaast kan een argument ook zwak zijn omdat hij verbonden is met een minder belangrijk onderdeel van de stelling. Ook kan een argument zwak zijn omdat in het argument correlatie wordt verward met een oorzakelijk verband. Bij deze categorie is het dus aan jou om de gegeven argumenten te beoordelen op sterkte/zwakte. Daarbij gebruik je de bovenstaande ‘criteria’.
Een Evaluatieopgave ziet er vaak zo uit:
Middelbare school leerlingen moeten meer mogelijkheid krijgen tot het volgen van culturele vakken zoals bijvoorbeeld dans of theater.
Argument: Ja, vaak moeten leerlingen deze lessen buiten school volgen, wat erg duur kan zijn. Dit zorgt ervoor dat dit voor gezinnen met weinig geld of veel kinderen niet mogelijk is. Als leerlingen dit op de middelbare school kunnen volgen, krijgen ze toch de kans om met dit soort vakken kennis te maken. Antwoordopties: Sterk argument – Zwak argument Het goede antwoord op deze voorbeeldopgave is ‘sterk argument’. Dit is een sterk argument omdat het inhoudelijk ingaat op het financiële aspect van culturele vakken. Ook legt het uit wat het voordeel kan zijn wanneer kinderen dit op school krijgen.
Tips voor het oplossen van Watson-Glaser opgaven
Gebruik alleen de informatie die gegeven is
Eén van de grootste valkuilen bij Watson-Glaser opgaven is het erbij halen van informatie die niet in de tekst staat. Probeer de conclusie, aanname, interpretatie etc. echt alleen te beoordelen op basis van de tekst of stelling die gegeven is. Ga daarnaast de informatie niet generaliseren. Probeer ook niet teveel door te denken.
Lees de informatie goed
Kijk niet direct naar de conclusie, aanname etc. die gegeven is, maar lees eerst goed de tekst of stelling. Kijk daarna naar de opgave zelf. Lees dan de tekst weer terug, nu met de conclusie, aanname etc. in je achterhoofd.
Laat je eigen mening achterwege
Een valkuil die vooral bij de aanname- en evaluatieopgaven voorkomt is het beoordelen of je het er zelf mee eens of oneens bent. Dit is echter niet de vraag. Vergelijk de aanname met de tekst die je leest en controleer alleen of deze aanname gedaan wordt of niet. Of jij het eens bent met de aanname speelt niet mee. Probeer alleen te kijken naar de kracht van het argument (sterk/zwak). Kijk niet of het argument waar is of niet. Dit is namelijk niet de vraag.
Oefening baart kunst!
Het is erg belangrijk om te oefenen voor een capaciteitentest.
Als je oefent kan je score hoger worden. Jouw jouw kans op het krijgen van die felbegeerde baan wordt daarmee ook groter. Oefen zoveel als je kunt. Dan kun je je opgaven sneller en efficiënter oplossen en krijg je een hogere score.
Omdat analogieën je verbale intelligentie meten, word je hier ook beter in als je andere verbale testen oefent.
Start direct met oefenen
LTP maakt assessments die geschikt zijn voor functies van verscheidene niveaus.
- ✓ 110+ tests
- ✓ 1700+ vragen
- ✓ 90 dagen geldig
Persoonlijkheidsvragenlijsten LTP
Tests LTP |
Uitleg en/advies |
| LTP Beïnvloedingsstijlentest | {roos van leary? effectief gedrag} |
| LTP Drijfveren | {prestatiemotivatie intrinsiek/extrinsiek} |
| LTP persoonlijkheidstest | Persoonlijkheidstest |
| LTP waardenvragenlijst | Werkwaardentest |
| LTP werkstijlen | Werkstijltest |
| LTP willen vragenlijst | {riasec} |
LTP Persoonlijkheidstest
De persoonlijkheidstest die standaard wordt gebruikt door LTP is een Big Five persoonlijkheidstest. Wil je weten hoe zo'n test en uitslag eruit ziet? Ben je benieuwd naar wat voor soort vragen je dan krijgt? Doe dan de Kerntyperingtest van 123test, ook deze is volledig gebaseerd op de Big Five persoonlijkheidstheorie.